Una matriz es una tabla cuadrada o rectangular de datos (llamados elementos) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. A una matriz con m filas y n columnas se le denomina matriz m-por-n (escrito m×n). Las dimensiones de una matriz siempre se dan con el número de filas primero y el número de columnas después.
Comúnmente se dice que una matriz m-por-n tiene un orden de m × n ("orden" tiene el significado de tamaño). Dos matrices se dice que son iguales si son del mismo orden y tienen los mismos elementos.
Ejemplo:
Dada la matriz:

que es una matriz 4x3. El elemento A[2,3] es el 7
La matriz:

Para sumar y restar matrices, éstas pueden ser, las dos cuadradas o las dos rectangulares. El número de filas y columnas de una han de ser igual al número de filas y columnas de la segunda.
Sumar:
Sumamos los valores que ocupan la misma posición.
El valor que se halla en la posición (1 1) de A con el valor de la posición (1 1) de la matriz B.
El valor que se halla en la posición (1 2) de A con el valor de la posición (1 2) de la matriz B.
El valor que se halla en la posición (1 3) de A con el valor de la posición (1 3) de la matriz B. De este modo haremos con el resto de las filas.
Vamos a sumar las matrices A y B:
Restar matrices:
Es lo mismo que en el caso anterior pero restando los valores que ocupan las mismas posiciones:

2.3 Clasificación de las matrices.
Según el aspecto de las matrices, éstas pueden clasificarse en:
=Matrices cuadradas =
Una matriz cuadrada es la que tiene el mismo número de filas que de columnas. Se dice que una matriz cuadrada n ð n es de orden n y se denomina matriz n-cuadrada. Ejemplo: Sean las matrices
Entonces, A y B son matrices cuadradas de orden 3 y 2 respectivamente.
=Matriz identidad=
Sea A = (ai j ) una matriz n-cuadrada. La diagonal (o diagonal principal) de A consiste en loselementos a11, a22, ..., ann. La traza de A, escrito trA, es la suma de los elementos diagonales.
La matriz n-cuadrada con unos en la diagonal principal y ceros en cualquier otra posición, denotada por I, se conoce como matriz identidad (o unidad). Para cualquier matriz A,
A· I = I ·A = A.
=Matrices triangulares=
Una matriz cuadrada A = (ai j ) es una matriz triangular superior o simplemente una matriz triangular, si todas las entradas bajo la diagonal principal son iguales a cero. Así pues, las matrices
son matrices triangulares superiores de órdenes 2, 3 y 4.
=Matrices diagonales=
Una matriz cuadrada es diagonal, si todas sus entradas no diagonales son cero o nulas. Se denota por D = diag (d11, d22, ..., dnn ). Por ejemplo,
son matrices diagonales que pueden representarse, respectivamente, por diag(3,-1,7) diag(4,-3) y diag(2,6,0,-1).
=Traspuesta de una matriz=
La traspuesta de una matriz A consiste en intercambiar las filas por las columnas y se denota por AT. Así, la traspuesta de
En otras palabras, si A = (ai j ) es una matriz m ð n, entonces AT = (aTij) es la matriz n ð m. La trasposición de una matriz cumple las siguientes propiedades:
- (A + B)T = AT + BT.
- (AT)T = A.
- (kA)T = kAT (si k es un escalar).
- (AB)T = BTAT.
=Matrices simétricas=
Se dice que una matriz real es simétrica, si AT = A; y que es antisimétrica, si AT = -A.
Ejemplo: Consideremos las siguientes matrices:
Podemos observar que los elementos simétricos de A son iguales, o que AT = A. Siendo así, A es simétrica. Para B los elementos simétricos son opuestos entre sí, de este modo B es antisimétrica. A simple vista, C no es cuadrada; en consecuencia, no es ni simétrica ni antisimétrica.
=Matrices ortogonales=
Se dice que una matriz real A es ortogonal, si AAT = AT A = I. Se observa que una matriz ortogonal A es necesariamente cuadrada e invertible, con inversa A-1 = AT.
Consideremos una matriz 3x3 arbitraria:
Si A es ortogonal, entonces:
=Matrices normales=
Una matriz es normal si conmuta con su traspuesta, esto es, si AAT = ATA. Obviamente, si A es simétrica, antisimétrica u ortogonal, es necesariamente normal.
Ejemplo:
=Matriz numérica=
Conjunto de números colocados en filas y en columnas.
=Matriz de orden (m,n)=
Conjunto de números reales, dispuestos en filas m, i en columnas n. Cada uno de los números que consta la matriz es un elemento, que se distingue entre los otros, por su posición.
=Subíndices=
Cada elemento tiene unos subíndices que sirven para indicar su posición dentro de la matriz. El primer indica la fila, y el segunda indica la columna.
=Orden de la matriz=
El número de filas y columnas de una matriz determina el orden de la matriz. El orden de la matriz está determinado por un par de números naturales; m y n.
Las filas son los números dispuestos en m horizontales. En el ejemplo, la primera fila estaría formada por los números [ 1 2 3 ].
Las columnas son los números dispuestos en n verticales. En el ejemplo, la primera columna estaría formada por los números [ 1 1 4 6 ].
Una matriz de orden (m,n) es el conjunto de números dispuestos en m filas y n columnas.
Siguiendo el mismo ejemplo, vemos que es una matriz 4x3. Se clasifica así porque la matriz contiene 4 filas y 3 columnas.
Si queremos señalar un elemento de la matriz, estos se distinguen por su posición, la cual queda definida por su fila y su columna.
Por ejemplo, si queremos dar la posición del número 7 (figura 1.1), sería de la siguiente forma: am,n es a2,3; m indica la fila en la cual se encuentra el número. Pasa exactamente lo mismo n, que indica la columna en la que se encuentra.
Transformaciones elementales en las filas, Las fases de una matriz, Rango de una matriz
Si se intercambian dos filas cualesquiera de una matriz dada, llamamos a esta operación una operación de transformación elemental en las filas de una matriz. Se denota por R¬ij¬¬, lo cual implica que se intercambian las filas i y j de la matriz dada. Esta operación también se denota por R¬i¬ <→ R-j¬.
Un punto digno de notar es que esta operación no es de naturaleza singular. De hecho se ha demostrado, que todas las matrices no singulares son el resultado de la transformación elemental en la fila de una matriz . Si esto es cierto, entonces podemos concluir, que para todas las matrices no singulares también tenemos una matriz inversa, la cual tampoco es singular y es también el resultado de la transformación elemental en la fila de una matriz. Esta matriz elemental se denomina la matriz identidad I y tenemos el resultado A x I = A-1
Existen tres operaciones básicas que pueden realizarse para transformar la fila de una matriz dada:
1. Intercambiar dos filas de la matriz dada, es decir, poner los elementos de una fila en el lugar del otro y viceversa.
2. Realizar la operación de multiplicación a cualquier fila de la matriz dada, multiplicando todas las entradas de esa fila con un elemento escalar.
3. Extraer un múltiplo común de todas las entradas de una fila y agregarlo a las entradas de la otra fila.
Podemos obtener la matriz cuadrada de una matriz, tomando, una parte de la matriz r x r de la matriz dada. Y llamamos a sus determinantes filas menores de r para la matriz de entrada. Entre todas las submatrices, el determinante que tenga el valor más alto distinto de cero, y que también es la submatriz más grande para la matriz dada, puede determinar el rango de la matriz dado que su orden igual al rango de la matriz actual.
Tomemos como ejemplo la siguente matriz:
A continuación se muestra las posibles submatrices de la matriz, que tienen sus determinantes como cero,
Esto significa que no podemos tener un rango de tres así que intentemos con la submatriz de orden dos, la cual da el rango de la matriz actual,
El determinante resulta ser 20, el cual es el más grande y por lo tanto, el rango de la matriz dada es dos.
Cálculo de la matriz inversa por el método de Gauss
Sea A una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos comoA-1, seguiremos los siguientes pasos:
1º Construir una matriz del tipo M = (A | I), es decir, A está en la mitad izquierda de M y la matriz identidad I en la derecha.
Consideremos una matriz 3x3 arbitraria
La ampliamos con la matriz identidad de orden 3.
2º Utilizando el método Gauss vamos a transformar la mitad izquierda, A, en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: A-1.
F2 - F1
F3 + F2
F2 - F3
F1 + F2
(-1) F2
La matriz inversa es:
Propiedades de la matriz inversa
(A · B)-1 = B-1 · A-1
(A-1)-1 = A
(k · A)-1 = k-1 · A-1
(A t)-1 = (A -1)t
2.6 Definicion de determinante de una matriz.En Matemáticas se define el determinante como una forma multilineal alternada de un cuerpo. Esta definición indica una serie de propiedades matemáticas y generaliza el concepto de determinante haciéndolo aplicable en numerosos campos. Sin embargo, el concepto de determinante o de volumen orientado fue introducido para estudiar el número de soluciones de los sistemas de ecuaciones lineales.
El determinante es una función que le asigna a una matriz de orden n, un único número real llamado el determinante de la matriz. Si A es una matriz de orden n, el determinante de la matriz A lo denotaremos por det(A) o también por (las barras no significan valor absoluto).
DEFINICIÓN 2.1(Determinante de una matriz de orden 1)
Si es una matriz de orden uno, entonces det(A)=a.
es una matriz de orden uno, entonces det(A)=a.
Si
DEFINICIÓN 2.2(Menores y cofactores de una matriz de orden n)
Sea A una matriz de orden
DEFINICIÓN 2.2(Menores y cofactores de una matriz de orden n)
Sea A una matriz de orden
2.7 propiedades de los determinantes.
Las propiedades de los determinantes, que enunciaremos a continuación, son válidas cualquiera que sea su orden. No obstante, para facilitar su comprensión, utilizaremos determinantes de orden 2 y 3. Las comprobaciones de las mismas se pueden hacer fácilmente desarrollando los determinantes.
1ª El determinante de una matriz cuadrada coincide con el determinante de su traspuesta, es decir: Det ( A ) = Det ( At )
2ª Si intercambiamos dos filas o dos columnas de una matriz cuadrada, su determinante cambia de signo aunque son iguales en valor absoluto.
3ª Si multiplicamos todos los elementos de una fila o columna de una matriz cuadrada por un número k, su determinante queda multiplicado por dicho número.
Como generalización de esta propiedad, si multiplicamos todos los elementos de una matriz cuadrada de orden n por un número k, su determinante queda multiplicado por kn, es decir: Det (k . A) = kn . Det ( A ).
4ª El determinante del producto de dos matrices cuadradas del mismo orden es igual al producto de los determinantes de dichas matrices: Det ( A . B ) = Det ( A ) . Det ( B ).
5ª Si una matriz cuadrada tiene todos los elementos de una fila o columna nulos, su determinante es cero.
6ª Si una matriz cuadrada tiene dos filas o dos columnas iguales su determinante es cero.
7ª Si una matriz cuadrada tiene dos filas o columnas proporcionales su determinante es cero.
8ª Si todos los elementos de una fila o columna de una matriz cuadrada se descomponen en dos sumandos, entonces su determinante es igual a la suma de dos determinantes que tienen en dicha fila o columna el primero y el segundo sumando respectivamente, siendo los restantes elementos iguales a los del determinante inicial.
9ª Si una fila o columna de una matriz cuadrada es combinación lineal de dos o más de las restantes filas o columnas, su determinante es cero.
10ª Si a una fila o columna de una matriz cuadrada se le suma otra paralela a ella, su determinante no varía.
11ª Si a una fila o columna de una matriz cuadrada se le suma otra paralela a ella multiplicada por un número, su determinante no varía.
Definición: Una matriz cuadrada se llama matriz
identidad si todos los componentes de su diagonal principal son
iguales a uno y todos los demás componentes que no están en la diagonal
principal son iguales a cero. La matriz identidad se representa con
la letra I (la letra i mayúscula).
Definición: Sea
A una matriz cuadrada n x n. Entonces una matriz B es la inversa
de A si satisface A ∙ B = I y B ∙ A =
I, donde I es la matriz identidad de orden n x n.
Ejemplo para discusión:
- La inversa de A se representa por A-1. Así
que A ∙ A-1 = A-1 ∙ A = I.
- No toda matriz cuadrada tiene una inversa.
- Si A tiene inversa, entonces decimos que A es invertible.
Teoremas:
- Sea A una matriz cuadrada n x n, entonces AI = IA = A.
- Si A es una matriz invertible, entonces A-1 es
invertible y (A-1)-1 = A.
- Si una matriz cuadrada A es invertible, entonces la inversa es
única.
- Sean A y B matrices de orden n x n invertibles. entonces
AB es invertible y (AB)-1 = B-1A-1.
Para hallar la inversa de una
matriz cuadrada comenzamos con la matriz A/I, donde I representa la matriz
identidad del mismo orden que la matriz A. Efectuamos
operaciones elementales con las filas de A/I hasta que la matriz A se
transforme en la matriz identidad I. Luego la matriz que contiene
los componentes a la derecha de la línea vertical es la inversa de A, esto es,
A-1.
2.9 Aplicación de matrices y determinantes.
Matrices cuadradas
Una matriz cuadrada es la que tiene el mismo número de filas que de columnas. Se dice que una matriz cuadrada n ð n es de orden n y se denomina matriz n-cuadrada.
Matriz identidad
Sea A = (ai j ) una matriz n-cuadrada. La diagonal (o diagonal principal) de A consiste en los elementos a11, a22, ..., ann. La traza de A, escrito trA, es la suma de los elementos diagonales.
La matriz n-cuadrada con unos en la diagonal principal y ceros en cualquier otra posición, denotada por I, se conoce como matriz identidad (o unidad). Para cualquier matriz A,
A· I = I ·A = A.
Matrices triangulares
Una matriz cuadrada A = (ai j ) es una matriz triangular superior o simplemente una matriz triangular, si todas las entradas bajo la diagonal principal son iguales a cero. Así pues, las matrices
Matrices diagonales
Una matriz cuadrada es diagonal, si todas sus entradas no diagonales son cero o nulas. Se denota por D = diag (d11, d22, ..., dnn ). Por ejemplo,
diag(3,-1,7) diag(4,-3) y diag(2,6,0,-1).
Traspuesta de una matriz
La traspuesta de una matriz A consiste en intercambiar las filas por las columnas y se denota por AT.
Así, la traspuesta de
1. (A + B)T = AT + BT.
2. (AT)T = A.
3. (kA)T = kAT (si k es un escalar).
4. (AB)T = BTAT.
Matrices simétricas
Se dice que una matriz real es simétrica, si AT = A; y que es antisimétrica,
si AT = -A.
Ejemplo:
Consideremos las siguientes matrices:
Para B los elementos simétricos son opuestos entre sí, de este modo B es antisimétrica.
A simple vista, C no es cuadrada; en consecuencia, no es ni simétrica ni antisimétrica.
Matrices ortogonales
Se dice que una matriz real A es ortogonal, si AAT = AT A = I. Se observa que una matriz ortogonal A es necesariamente cuadrada e invertible, con inversa A-1 = AT.
Consideremos una matriz 3 ð 3 arbitraria:


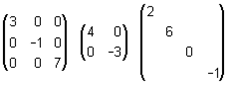








No hay comentarios.:
Publicar un comentario